線形回帰のカーネルトリック
前提
関数は以下のものにノイズを加える
$$ y=x3+\epsilon $$
見ての通り線形回帰だとうまくいきそうにないのでガウシアンカーネルで回帰を行う
また、コスト関数には誤差の総和を用い解析的に解く
まずは線形回帰
import numpy as np import matplotlib.pyplot as plt size = 25 #サンプル数 x = np.linspace(-6, 6, size) y_truth= (-0.05 * x ** 4) + ( 0.1 * x ** 3) + (-0.5 * x ** 2) + (0.6 * x ) np.random.seed(0) y_noise = y_truth + np.random.randn(size) * 10.0 plt.plot(x, y_truth, color='#aaaaaa') plt.scatter(x, y_noise, color="#aaaaaa") w = (1 / np.dot(x, x) * x).dot(y_noise) y_predict = w * x plt.plot(x, y_predict, color="r") plt.scatter(x, y_predict, color="r")
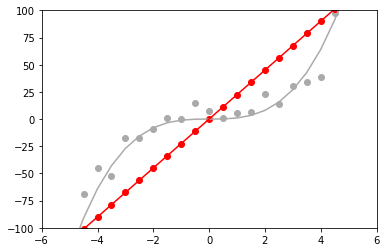
次に正則化していないカーネル
import numpy as np import matplotlib.pyplot as plt size = 25 # サンプル数 x = np.linspace(-6, 6, size) y_truth= x**3 np.random.seed(0) # ノイズ固定 y_noise = y_truth + np.random.randn(size) * 10.0 # 本来のデータ plt.plot(x, y_truth, color='#aaaaaa') plt.scatter(x, y_noise, color="#aaaaaa") # ガウシアンカーネル def kernel(x1, x2, beta=1.0): return np.exp(- beta * (x1 - x2)**2) # グラム行列 K = np.zeros((size, size)) for i in range(size): for j in range(size): K[i,j] = kernel(x[i], x[j]) # 解析計算 alpha = np.linalg.inv(K) * y_noise # 計算したパラメータをもとに予測 y_predict_kernel = np.zeros(length) for _x, a in zip(x, alpha): y_predict_kernel += a * kernel(_x, _x) # プロット plt.plot(x, y_predict_kernel, color="b") plt.scatter(x, y_predict_kernel, color="b") plt.xlim([-6,6]) plt.ylim([-50, 50])

予想通りぐちゃぐちゃ
正則化を行って計算
size = 25 # サンプル数 x = np.linspace(-6, 6, size) y_truth= x**3 np.random.seed(0) # ノイズ固定 y_noise = y_truth + np.random.randn(size) * 10.0 # 本来のデータ plt.plot(x, y_truth, color='#aaaaaa') plt.scatter(x, y_noise, color="#aaaaaa") # ガウシアンカーネル def kernel(x1, x2, beta=1.0): return np.exp(- beta * (x1 - x2)**2) # グラム行列 K = np.zeros((size, size)) for i in range(size): for j in range(size): K[i,j] = kernel(x[i], x[j]) # 解析計算 (アルゴリズム的にはここに単位行列を足しただけ) alpha = np.linalg.inv(K + np.identity(size)) * y_noise # 計算したパラメータをもとに予測 y_predict_kernel = np.zeros(length) for _x, a in zip(x, alpha): y_predict_kernel += a * kernel(_x, _x) # プロット plt.plot(x, y_predict_kernel, color="b") plt.scatter(x, y_predict_kernel, color="b") plt.xlim([-6,6]) plt.ylim([-50, 50])
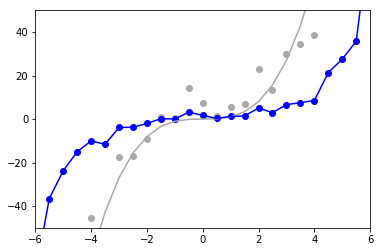
正則化項が働いて多少汎化された。
それで
モデルを通常の線形パラメータとは違うものに置き換えていることや、ガウシアンカーネルの次元数が無限にあることにより、正則化による影響が直感的にわかりにくいけど、うまくはいっているみたい。